
これは、「BASE Advent Calendar 2018」の6日目の記事です。
DataStrategyの齋藤(@pigooosuke)が担当します。
はじめに
機械学習エンジニアの人は、分類や回帰などの課題に取り組むにあたって、偉い人や導入先の部門から「その予測どれぐらい外れるの?」「学習モデルの予測に対してどうリスク評価をすればいいの?」と尋ねられることはありませんか? そのような場面で活躍するかもしれないQuantile Regression(分位点回帰)のお話をします。
回帰モデルの評価
カテゴリーを予測するような分類問題では、各クラスでの精度を確認することはできます。しかし、売上や何かしらの値を予測する回帰問題では、そのモデルにおける特定地点での単一の予測値しか出力することが出来ず、その分布を把握することは単純ではありません。
# scikit-learnの線形回帰サンプル >>> import numpy as np >>> from sklearn.linear_model import LinearRegression >>> X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]]) # 入力値のセット >>> y = np.dot(X, np.array([1, 2])) + 3 # 正解データ >>> reg = LinearRegression().fit(X, y) >>> reg.predict(np.array([[3, 5]])) # 入力[3, 5]に対して、予測値は1つ array([16.])
ここで説明にあたって予測の確度という言葉を使うと定義が甘いのでもう少し分解します。回帰予測の範囲を把握する上でよく出てくるのは、この2種類ではないでしょうか。混同しないように事前に再確認しましょう。
- 信頼区間 Confidence interval
- ex. 95%信頼区間。こちらは、同じ条件で100回測定したら、計算した回帰曲線がその信頼区間内に収まった測定が95回ありましたという意味になります。
- 予測区間 Prediction interval
- ex. 95%予測区間。こちらは、今後観測しうるデータが100回出現したら、予測区間内に収まる観測が95回ありましたという意味になります。
下図は、標本に対して回帰曲線を計算したものです。
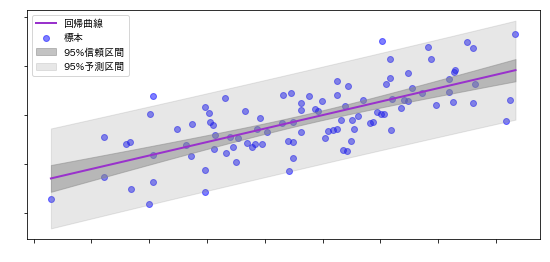
回帰曲線は信頼区間に収まり、標本は予測区間に収まります。
基本的には予測区間のほうが信頼区間の外側に位置します。
使い分けとしては、
- モデルそのものの精度を測りたいのであれば
信頼区間 - モデルにおける特定地点での予測値のばらつきを調べたいのであれば
予測区間
が目安になると思います。 今回お話をするQuantile Regressionは、予測区間を説明するために利用します。
Quantile Regression ~ 分位点回帰 ~
Quantileとは、日本語で四分位のことです。データをソートして区切った場合、それぞれのデータが上位何%に位置するのかを表現するときに使います。 2 quantileは、中央値と一致します。
0 quantile = 0 %ile (percentile: パーセンタイル) 1 quantile = 25 %ile 2 quantile = 50 %ile = median(中央値) 3 quantile = 75 %ile 4 quantile = 100 %ile
Quantile Regressionは、線形回帰の損失関数を拡張したもので、通常のように二乗誤差を求めて平均値を最適化するのではなく、予め設定したquantile(percentile) での損失関数を最適化していきます。年収など偏りがある分布を平均値ではなく、中央値で確認したい場合に利用されます。用途としても、単純に各分位点での予測値の開きをみるだけでなく、例えば、年収or家賃の大小によって格差を図る指標がどれぐらい変化するのかを比較することによって変数の理解に繋がることもあり、社会学や経済学の分野で活用される事例が多くあります。
ちなみに、Quantile Regressionの推定には、check functionと呼ばれる常に絶対値を取るインジケーター関数を利用して、
以下の損失関数を最適化していきます。
手短に説明すると、正解値と予測値の差が正のときに、 負のとき(反転するので正確には正)に
が重み付けされた和をLossとしています。
導出を詳しく知りたい人はこちらのリンクが詳しいです。
- 原著(pdf) QUANTILE REGRESSION : ROGER KOENKER
- wikipedia, Quantile Regression
- Statistics/Numerical Methods/Quantile Regression
理論的な部分の解説
リンク先を見ても細かな部分の省略が多かったので、勉強ついでに自分でも導出をやってみました。興味がなければ読み飛ばし推奨です。
を確率変数、
を平均値、
をquantile(percentile)、
を分布の中心として定義した場合、平均は誤差の平方和の最小値で表せるように、中央値は絶対偏差和の最小値で表すことができます。
が
以下のときの
を以下のように累積分布関数
を用いて定義します。
これを逆関数で表すとこうなります。
上で中央値を定義しましたが、これを一般化すると、
]
ここでのが最初に出てきた非負となるインジケーター関数です。
このインジケーター関数を一行で表現するとこうなります。
確率変数のときにおける、確率密度関数を
、累積分布関数を
とします。そして、離散値として
で、連続値として
で表現すると、それぞれ以下の通りになります。
上記に対し、で微分し、左辺を0と置いたとき、
となり、と分位点
が等しくなりました。
Pythonで試してみる
Python系ライブラリのいくつかでは、このQuantile Regressionの損失関数がサポートされており、サンプルとして少し紹介してみます。
みんな大好きscikit-learn
import numpy as np import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor #### sin波にノイズを加えたデータセットでやってみます。 n = 300 # 標本数 noise = 0.2 # noiseの強さ np.random.seed(1) x = np.linspace(0, 2*np.pi, n) y = np.sin(x) + noise * np.random.randn(n) x = x.reshape(-1, 1) # 95%予測区間を求めるため、上限・下限ともに5%を2で等分した0.025, 0.975の位置で予測する alpha = 0.975 # model 定義 clf = GradientBoostingRegressor(loss='quantile', alpha=alpha, n_estimators=250, max_depth=3, learning_rate=.1, min_samples_leaf=9, min_samples_split=9) # 上限の予測 clf.fit(x, y) y_upper = clf.predict(x) # alphaを反転して下限の予測 clf.set_params(alpha=1.0 - alpha) clf.fit(x, y) y_lower = clf.predict(x) # 損失関数を最小2乗法に設定して予測 clf.set_params(loss='ls') clf.fit(x, y) y_pred = clf.predict(x) # vizualization fig = plt.figure(figsize=(8, 4)) plt.plot(x, y, 'b.', markersize=10, label="標本") plt.plot(x, y_upper, 'k-') plt.plot(x, y_lower, 'k-') plt.plot(x, y_pred, 'r-', label='予測値') plt.fill(np.concatenate([x, x[::-1]]), np.concatenate([y_upper, y_lower[::-1]]), alpha=.5, fc='b', ec='None', label='95%予測区間') plt.legend(loc='upper right') plt.show()

現在は、アンサンブルのGradientBoostingRegressorでしか、この損失関数は設定出来ません。
ちなみに、以前から線形モデルに対してQuantile Regressionを追加しようという動きはあるようです。続報が待たれますね。 https://github.com/scikit-learn/scikit-learn/issues/3148
勾配ブースティングのLightGBM
import lightgbm as lgb # 95%予測区間を求めるため、上限・下限ともに5%を2で等分した0.025, 0.975の位置で予測する alpha = 0.975 # model 定義 clf = lgb.LGBMRegressor(objective='quantile', alpha=alpha, n_estimators=250, max_depth=3, learning_rate=.1, min_samples_leaf=9, min_samples_split=9) # 上限の予測 clf.fit(x, y) y_upper = clf.predict(x) # alphaを反転して下限の予測 clf.set_params(alpha=1.0 - alpha) clf.fit(x, y) y_lower = clf.predict(x) # 損失関数を最小2乗法に設定して予測 clf.set_params(objective='regression') clf.fit(x, y) y_pred = clf.predict(x) # vizualization fig = plt.figure(figsize=(8, 4)) plt.plot(x, y, 'b.', markersize=10, label="標本") plt.plot(x, y_upper, 'k-') plt.plot(x, y_lower, 'k-') plt.plot(x, y_pred, 'r-', label='予測値') plt.fill(np.concatenate([x, x[::-1]]), np.concatenate([y_upper, y_lower[::-1]]), alpha=.5, fc='b', ec='None', label='95%予測区間') plt.legend(loc='upper right') plt.show()

実際、scikit-learnに実装されている損失関数自体も中身は
pred = pred.ravel() diff = y - pred alpha = self.alpha mask = y > pred if sample_weight is None: loss = (alpha * diff[mask].sum() - (1.0 - alpha) * diff[~mask].sum()) / y.shape[0]
と、非常にシンプルな構造になっています。 ちなみに、LightGBMの実装は以下のようになっていました。
class QuantileMetric : public RegressionMetric<QuantileMetric> { public: explicit QuantileMetric(const Config& config) :RegressionMetric<QuantileMetric>(config) { } inline static double LossOnPoint(label_t label, double score, const Config& config) { double delta = label - score; if (delta < 0) { return (config.alpha - 1.0f) * delta; } else { return config.alpha * delta; } } inline static const char* Name() { return "quantile"; } };
それぞれのleaf_valueでの正解と予測の差に対して重みを付けているだけなので、根本は同じですね。
ただし、もう一つの勾配ブースティング代表格のXgboostでは標準実装されておらず、自分で損失関数を設定する必要がありそうです。 興味がある人は自作してみると面白いかもしれませんね。
今回は、回帰モデルの出力を説明するという点でQuantile Regressionを紹介しました。 回帰モデルの出力に関して説明を求められたときの一つの手法として覚えておくと良さそうですね。
明日は、id:lllitchi さんがデザインについて語ってくれます。お楽しみに!