
この記事はBASE Advent Calendar 2019の20日目の記事です。
DataStrategyの岡が担当します。
Prophet is 何?
ProphetはFacebook社製の時系列予測ライブラリです。RとPythonから利用でき下記gitで公開されています。 https://github.com/facebook/prophet
分析者仲間の間で「時系列予測ならまずこれを使っとけ」と言われるくらい高精度らしいのですが、私自身がイマイチ理論を把握してない & ググってもさらっとした解説の日本語ドキュメントしかない印象です。
Prophetの元となる論文は下記にて公開されています。 https://peerj.com/preprints/3190.pdf
冒頭だけ読むと、時系列分析の知見のない人でもドメイン知識を組み込みながら予測ができるようなツールを目指して開発されたようです。論文タイトルが「Forecasting at Scale」となっていて「Scale」というのはここでは「誰でも使える、スケールしやすい予測ツール」みたいな意味で使われています。
論文に書かれているProphetのモデル式をしっかり理解できるように丁寧になぞっていこう、というのがこの記事の趣旨です。
モデル式の概要
時系列データは、トレンド + 季節要因 + ノイズ などの複数の要素から成り立っていて、これらの要素に分解することで理論値の予測ができる、という考え方があります。
Prophetでは、時系列は下記のような構成要素をもつと捉えています。
さらに、時系列はこれらの要素の和と捉え下記のようなモデル式を組み立てています。
このモデル式を理解するため、誤差項以外の3要素を一つずつ見ていきます。
1.  : トレンド関数
: トレンド関数
まず ですが
- ロジスティック非線形トレンド
- 線形トレンド
の2種類があります。1のほうから読み解いてみます。
1-1. ロジスティック非線形トレンド
ごく単純化すると下記のように表されます。
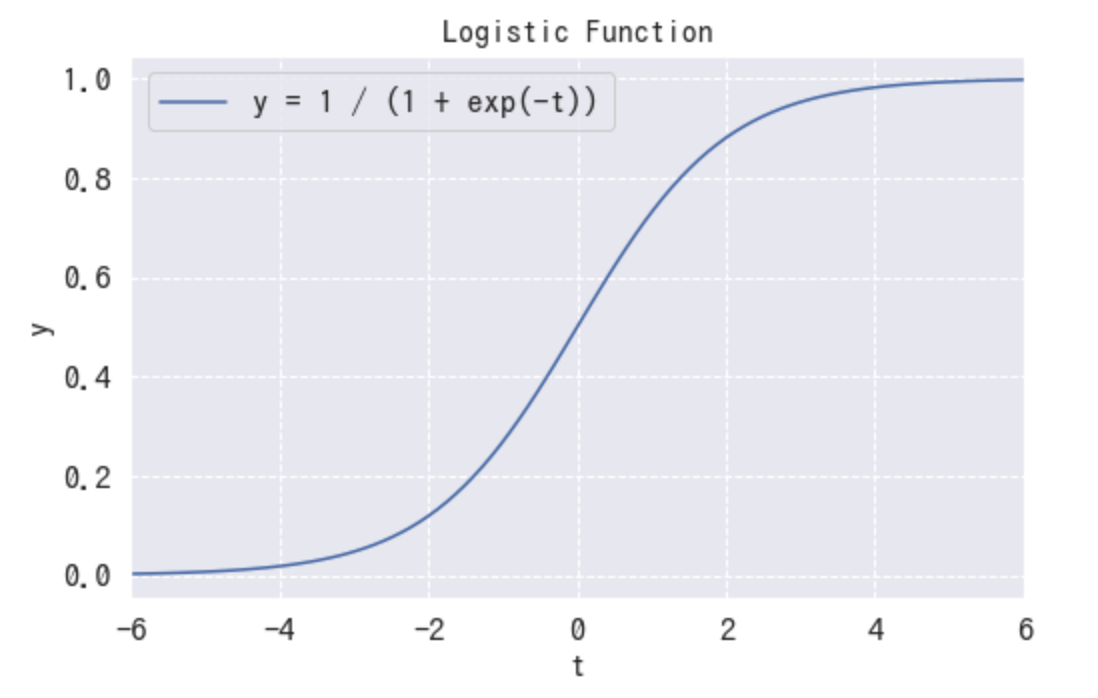
のとき
のとき
となり出力 の下限と上限が決まっています。この基本となる式(2)に一つずつ
の3要素を継ぎ足してトレンド関数の形に近づけていきます。
生物の個体数やプログラムのバグ発見数など、初めは少ない → 途中は多くなる → その後また少なくなる
という流れを持つ現象はロジスティック曲線で説明されることがあります。
生物の個体数などには何かしら上限数があると考えられ、トレンド関数では をつけることでこの上限を設定しています。
トレンド関数にならって、ロジスティック関数(式(2))の分子を に変えてみます。
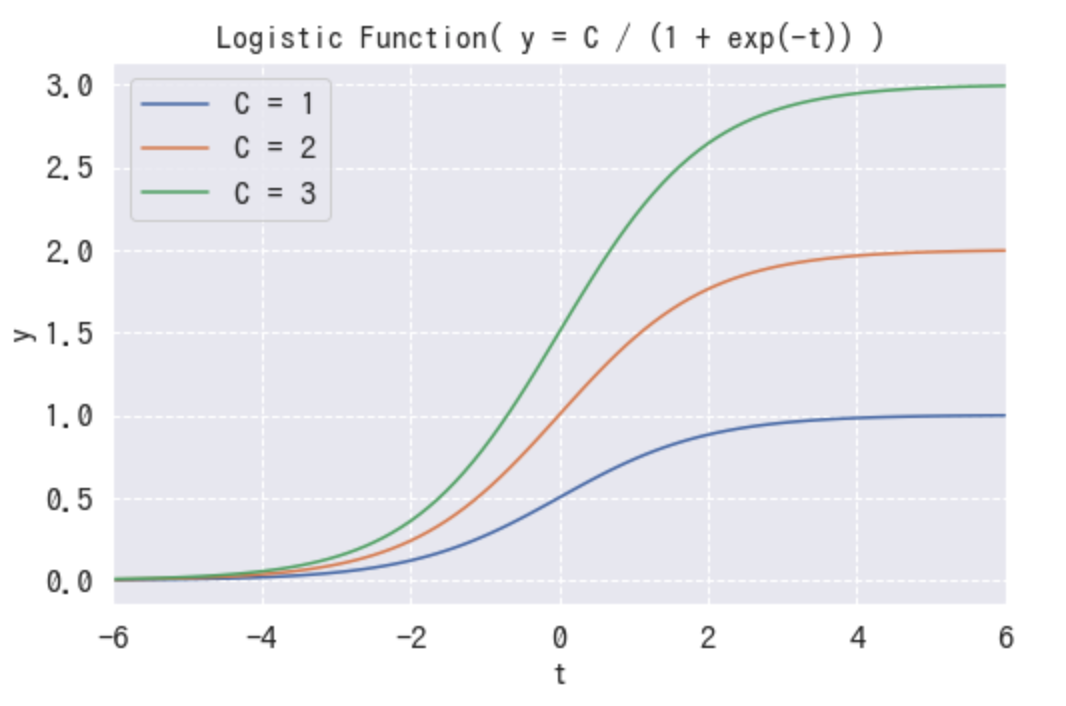
のmax値が
の値に等しくなり、これで上限を設定できるようになりました。
続いて
を加えてみましょう。
を固定した状態で、
の値を-1, 0.5, 1,...と変化させると曲線は下図のように変化します。
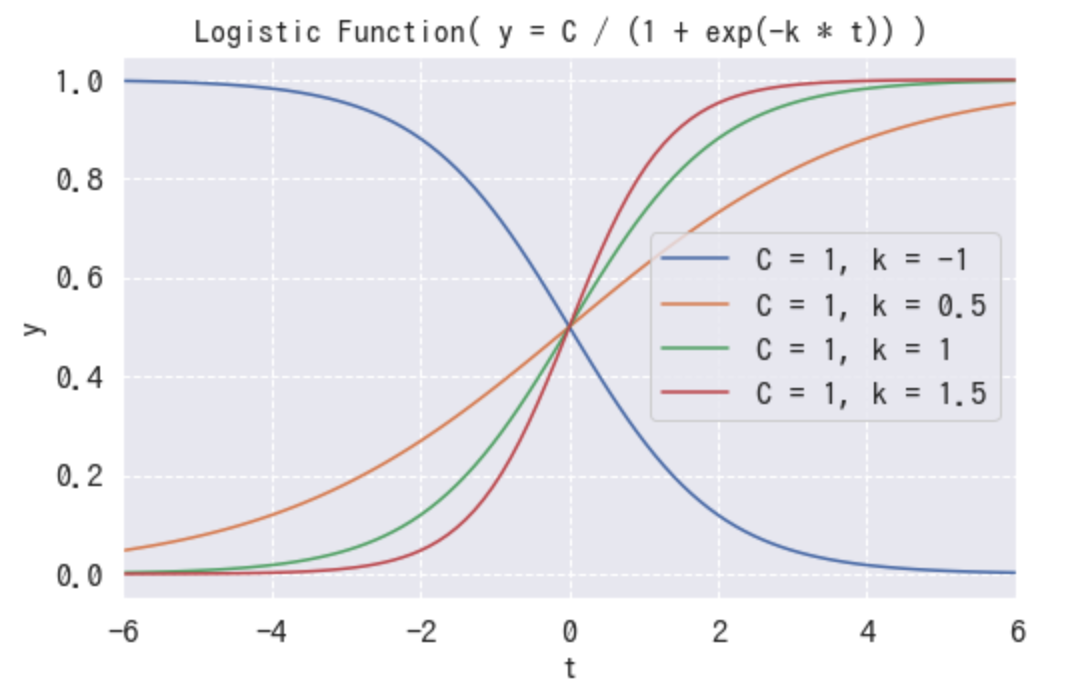
が大きいほど曲線が急になり、小さいほど緩やかになるのが見て取れます。
の時はもはや減少関数となり、
は「傾き」のようなものだと解釈できます。
生物の個体数でいうなら、成長スピードの早い群はより早く上限に達し、成長の遅い群は上限に達するのも遅い、といった知見をパラメタ で表現できます。
続いて、 を追加していきます。
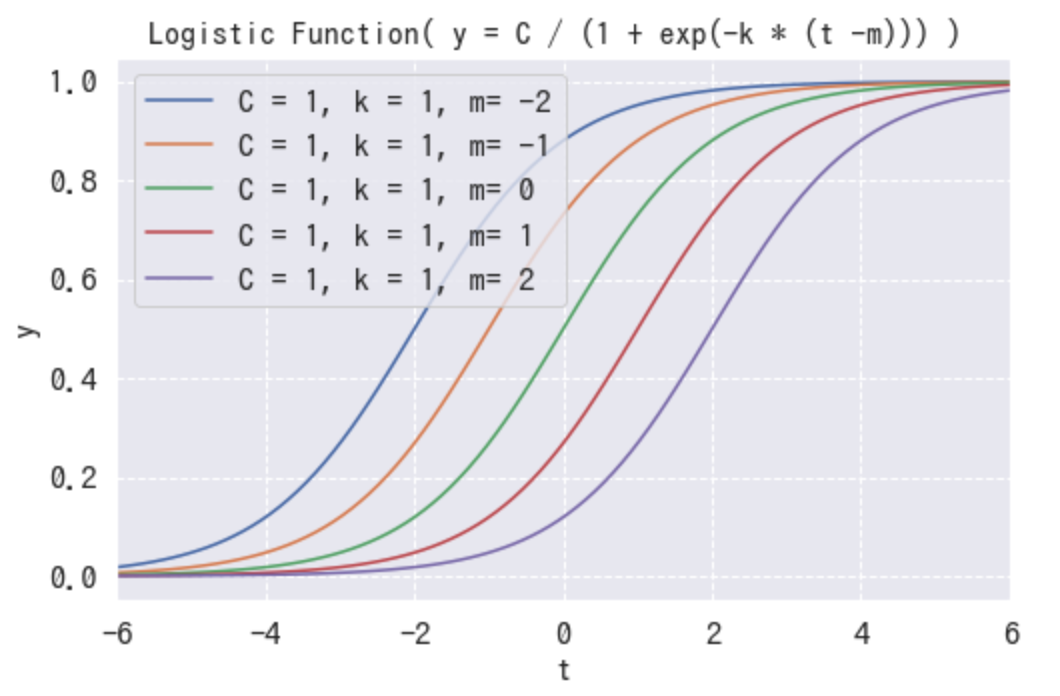
は
の値をダイレクトに減算する式になっているので単に曲線が左右に動くだけですね。言い換えると同じ
でも
の値を上下させる働きを持っています。線形回帰でいうところの切片のようなものとイメージして下さい。
以上で下記の式の説明は終わりです。
は各
時点で異なる上限を設定できるようになった、というだけの話なので説明はこれくらいに留め、
のほうをじっくり見ていきます。
は転換期のようなものを迎えた場合かなり異なったレートに変化するはず、というニュアンスを数式で表現したいとします。仮にそのような転換点がS個あったとして、そのときの
時点を
結局 は各変更点
を迎えるごとにひとつずつ変更点のフラグが立つだけのベクトルと言えます。これと先ほど定義した変更率
のベクトル、
を組み合わせると式(3)は、
import numpy as np from matplotlib import pyplot as plt T = np.linspace(-6, 6, 100) S = np.array([-3, 1, 3]) # -3, 1, 3の時点で成長率に変化が起きる delta = np.array([0.1, 0.3, -0.6]) # 各S時点での成長率の変更率 def logistic_trend(T, S, delta, k=1, C=1, m=0): a = np.vstack([np.where(S < t, 1, 0) for t in T]) y = C / (1 + np.exp(-(k + (a * delta).sum(axis=1)) * (T - m))) return y out = logistic_trend(T, S, delta, k=0.1, m=0) plt.plot(T, out) plt.xlabel("t", fontsize=16) plt.ylabel("y", fontsize=16) # plot change point ymax = out.max() ymin = out.min() plt.vlines( S, ymin=ymin, ymax=ymax, linestyle='dashed', color='gray', label='change point' ) plt.legend() plt.show()
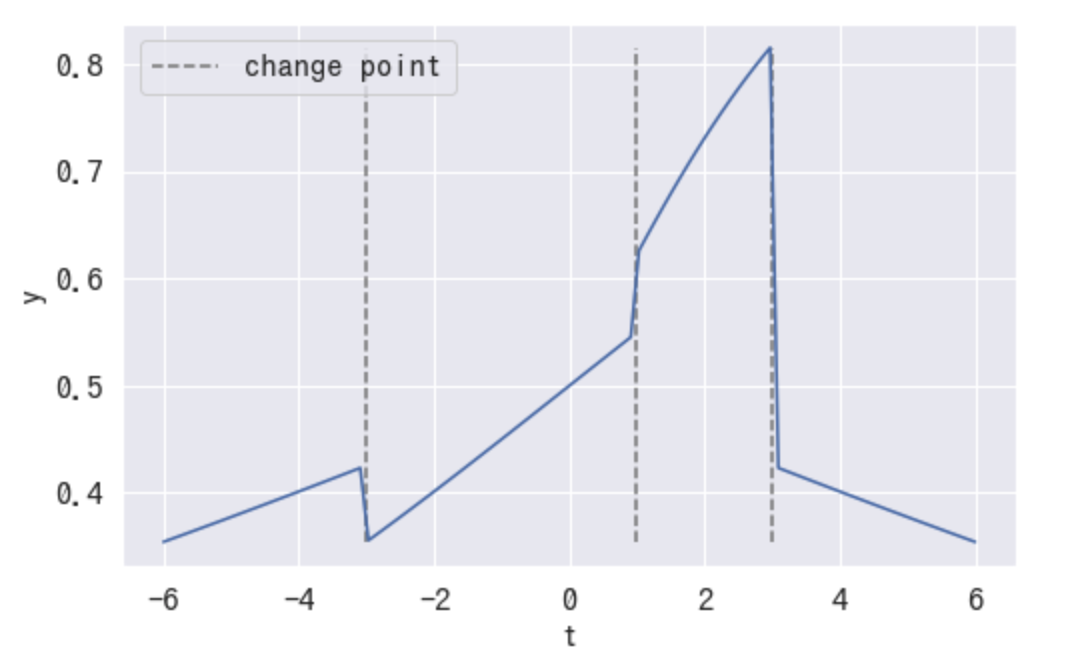
変化点ごとに曲線が切れてしまってます。
さきほど は「傾き」のようなもので、
は「切片」のようなものだと説明しました。
のようなシンプルな一次関数と同じように考えて欲しいのですが、傾きaは
T1 = np.linspace(-6, -2, 30) T2 = np.linspace(-2, 6, 70) def sample_linear(T, a=1): y = a * T return y out1 = sample_linear(T1, a=1) out2 = sample_linear(T2, a=-1) plt.plot( np.hstack([T1, T2]), np.hstack([out1, out2]), ) plt.xlabel("t", fontsize=16) plt.ylabel("y", fontsize=16) plt.show()
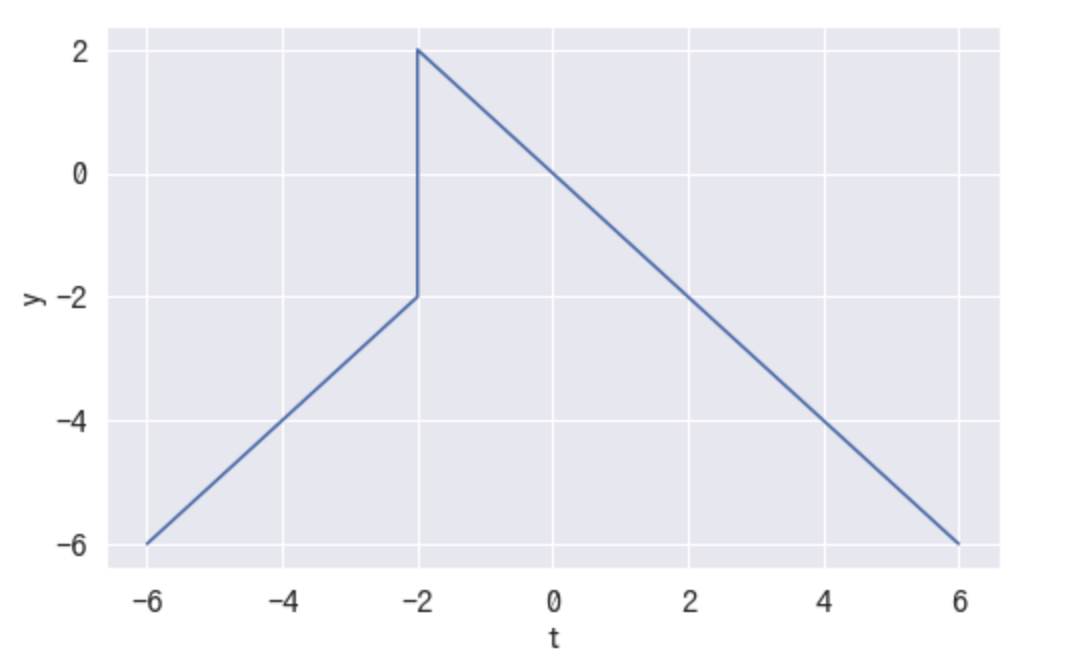
この場合は切片bを調節することで連続した直線が得られますが、話をトレンド関数に戻して考えるとオフセット項mを調整すれば連続した曲線が得られそうです。
転換点S個だけ調節する値が必要なので と同じく
この修正を先ほどのコードに加えると下記のようにグラフ化できます。
T = np.linspace(-6, 6, 100) S = np.array([-3, 1, 3]) delta = np.array([0.1, 0.3, -0.6]) def logistic_trend(T, S, delta, k=1, C=1, m=0): a = np.vstack([np.where(S < t, 1, 0) for t in T]) gamma = np.zeros(S.shape) for j in range(0, gamma.shape[0]): gamma[j] = (S[j] - m - gamma[:j].sum()) * (1 - ((k + delta[:j].sum()) / (k + delta[:j + 1].sum()))) y = C / (1 + np.exp(-(k + (a * delta).sum(axis=1)) * (T - (m + (a * gamma).sum(axis=1))))) return y out = logistic_trend(T, S, delta, k=0.1, m=0) plt.plot(T, out) plt.xlabel("t", fontsize=16) plt.ylabel("y", fontsize=16) # plot change point ymax = out.max() ymin = out.min() plt.vlines( S, ymin=ymin, ymax=ymax, linestyle='dashed', color='gray', label='change point' ) plt.legend() plt.show()
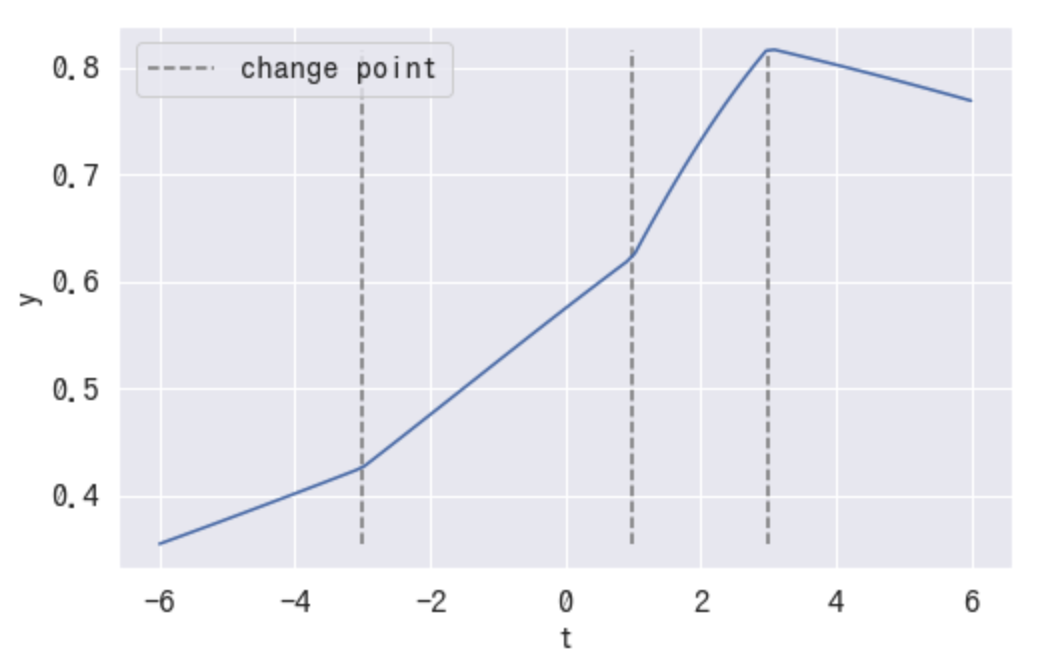
これで連続した曲線が得られました。
1-2. 線形トレンド
線形トレンドは下記の式で表されます。
T = np.linspace(-6, 6, 100) S = np.array([-3, 1, 3]) delta = np.array([0.1, 0.3, -0.6]) def linear_trend(T, S, delta, k=1, m=0): a = np.vstack([np.where(S < t, 1, 0) for t in T]) gamma = -S * delta y = (k + (a * delta).sum(axis=1)) * T + (m + (a * gamma).sum(axis=1)) return y out = linear_trend(T, S, delta, k=0.1, m=0) plt.plot(T, out) plt.xlabel("t", fontsize=16) plt.ylabel("y", fontsize=16) # plot change point ymax = out.max() ymin = out.min() plt.vlines( S, ymin=ymin, ymax=ymax, linestyle='dashed', color='gray', label='change point' ) plt.legend() plt.show()
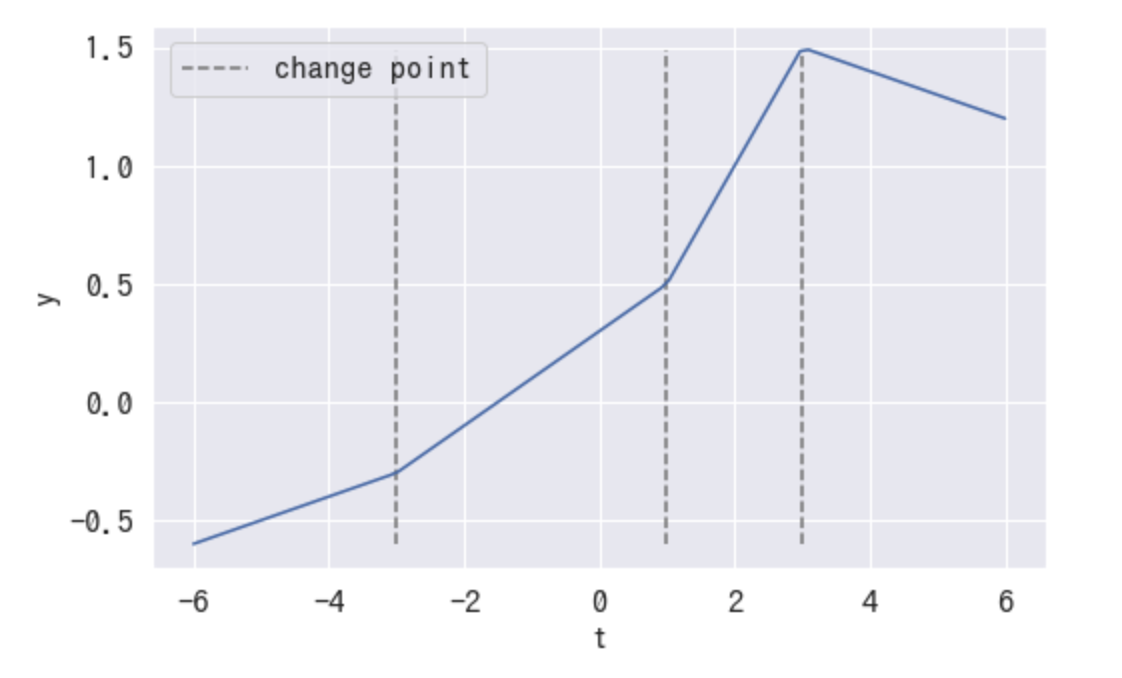
1-3. 変化点の自動検出
変化点 はユーザー自身で設定することもできますが、スパース推定のようなことをして自動検出も可能です。
論文によると変化点
の上限数を多めにとり、各点の変更率
に対し
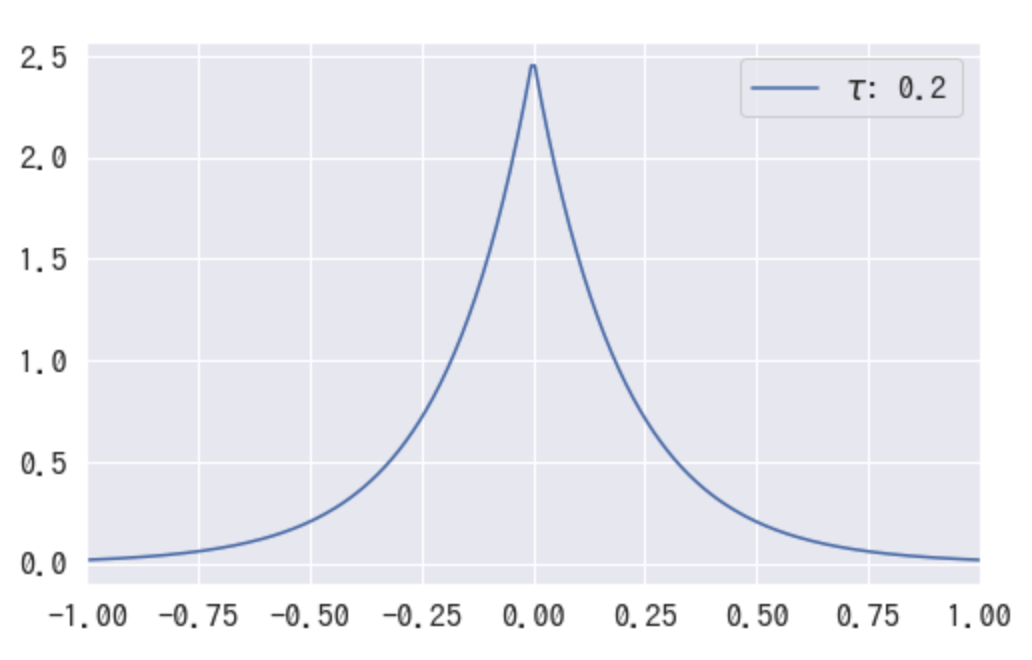
正規分布よりも0付近の値が出現しやすくなっている、という特徴がありそうです。
さらに の部分を変化させると下記のような分布が得られます。
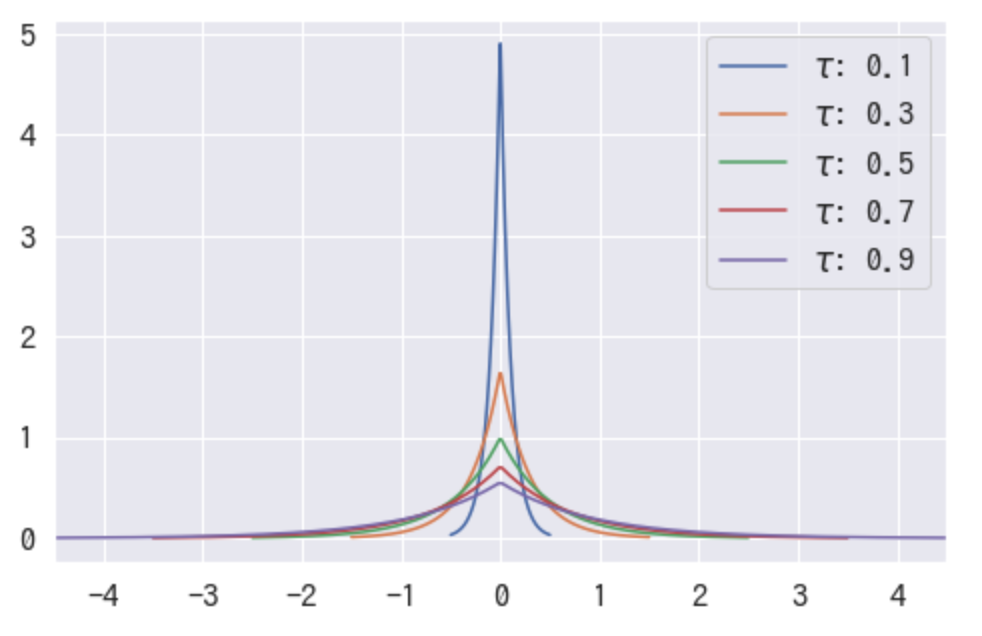
が0に近づくにつれ、ほとんど0の値しか出現しない(スパースな)分布になっていることが見て取れます。
ここまでの話をまとめると、、、変更率 にラプラス分布を仮定すると、多めの変更点をとっておいても変更率はほぼ0になり、かつ稀に大きな変更率が発生するという事象を再現することができます。また、変更率の大きさそのものは
を小さく調整することで抑えることが可能になります。
1-4. トレンド関数の予測
ここまで扱ってきた変更率 ですが、実際の予測の際にはどのような値を取ると良いでしょうか。論文を読むと、時系列データを予測する際に変更率
を下記のようにシミュレーションさせるとあります。
まずラプラス分布のスケール を決定するためベイズ推定で事後分布を得るか、そうでなければ最尤推定的に解いて
を分布のスケールとします。この場合の
は過去に出現した変更率
の絶対値の平均です。
過去の時系列の長さが 個、そのうち成長率の変更のあった時点が
個と定義したので、変更点の発生確率は
、発生しない確率は
と言えます。
これらを踏まえ、論文では将来の
について下記のように定義しています。
with probabilityの略なので
の確率で
の確率で
は
の分布に従う乱数
という意味になります。
まとめると、未来の変更率 を求めるには、まず
の確率で
が0になるかラプラス分布に従う乱数となるかが決まり、ラプラス分布に従う場合は その分布の乱数が変更率
となる...以上のプロセスを予測したい時点ぶん繰り返すことになります。
この一連のシミュレーションをコードで書くと下記のようになります。トレンド関数にはロジスティックのほうを用いています。
class LogisticTrendEstimator: def fit(self, T, S, delta, k=1, C=1, m=0): self._T = T self._S = S self._delta = delta self._k = k self._C = C self._s_freq = len(S) / len(T) self._mu_delta = np.abs(delta).mean() self._y, self._gamma = self._logistic_trend(T, S, delta, k, C, m) def _logistic_trend(self, T, S, delta, k=1, C=1, m=0): a = np.vstack([np.where(S < t, 1, 0) for t in T]) gamma = np.zeros(S.shape) for j in range(0, gamma.shape[0]): gamma[j] = (S[j] - m - gamma[:j].sum()) * (1 - ((k + delta[:j].sum()) / (k + delta[:j + 1].sum()))) y = C / (1 + np.exp(-(k + (a * delta).sum(axis=1)) * (T - (m + (a * gamma).sum(axis=1))))) return y, gamma def forecast(self, length=10, seed=None): np.random.seed(seed=seed) # generate future change point, and its change rate occurrence = np.random.binomial(n=1, p=self._s_freq, size=length) generated_s = np.where(occurrence == 1)[0] + self._T.max() generated_delta = np.random.laplace(0, self._mu_delta, generated_s.shape[0]) # predict future = np.arange(length) + self._T.max() future_y, _ = self._logistic_trend( T=future, S=generated_s, delta=generated_delta, k=self._k, C=self._C, m=self._gamma[-1] ) # plot y plt.plot(self._T, self._y, c='steelblue', label='past') plt.plot(future, future_y, c='darkorange', label='predict') plt.xlabel("t", fontsize=16) plt.ylabel("y", fontsize=16) # plot change point ymax=np.max([self._y.max(), future_y.max()]) ymin=np.min([self._y.min(), future_y.min()]) plt.vlines( np.hstack([self._S, generated_s]), ymin=ymin, ymax=ymax, linestyle='dashed', color='gray', label='change point' ) plt.legend() plt.show() return future_y T = np.arange(100) S = np.array([20, 60, 80]) delta = np.array([-0.03, 0.01, 0.02]) estimator = LogisticTrendEstimator() estimator.fit(T=T, S=S, delta=delta, k=0.01, m=0) pred = estimator.forecast(length=100, seed=123)
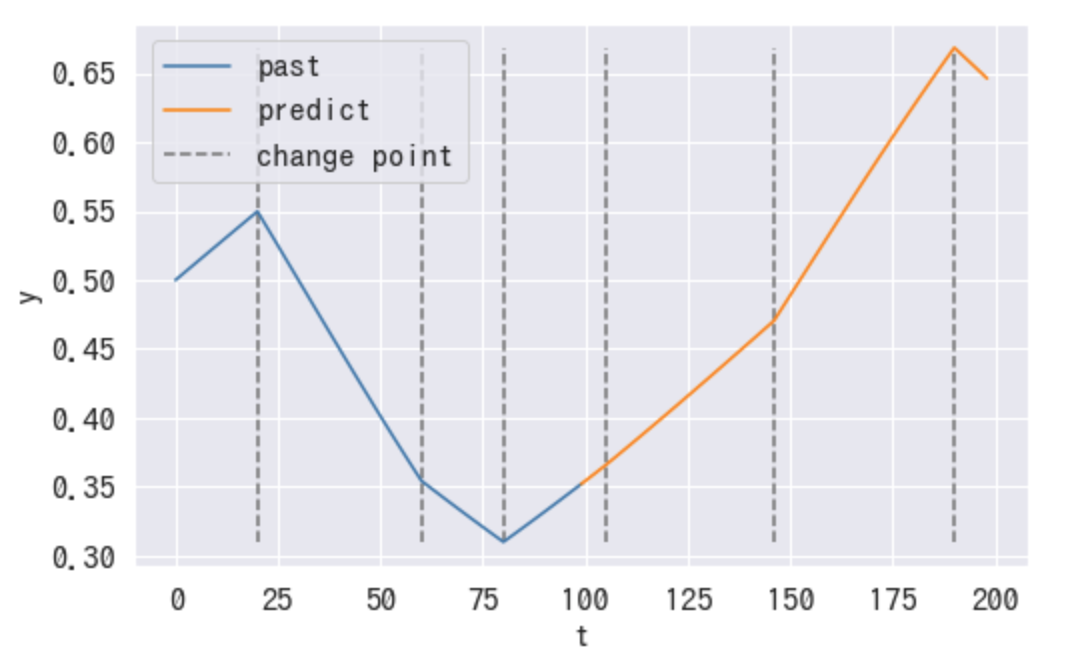
2.  : 季節変化
: 季節変化
次に季節変化を表現する下記の式を理解していきます。
英語の直訳で「季節変化」と書きましたが、意味的には季節を含め、週、月、年といったあらゆる周期性を で扱えます。
季節による変動がある → 周期性がある → 信号処理っぽく表現できる、という発想で は下記のように一般的なフーリエ級数で表現されています。
この式を理解するために、まずフーリエ級数展開の気持ちを簡単に復習します。
フーリエ級数展開について
下記のような曲線をどうにかして関数で表したいとします。
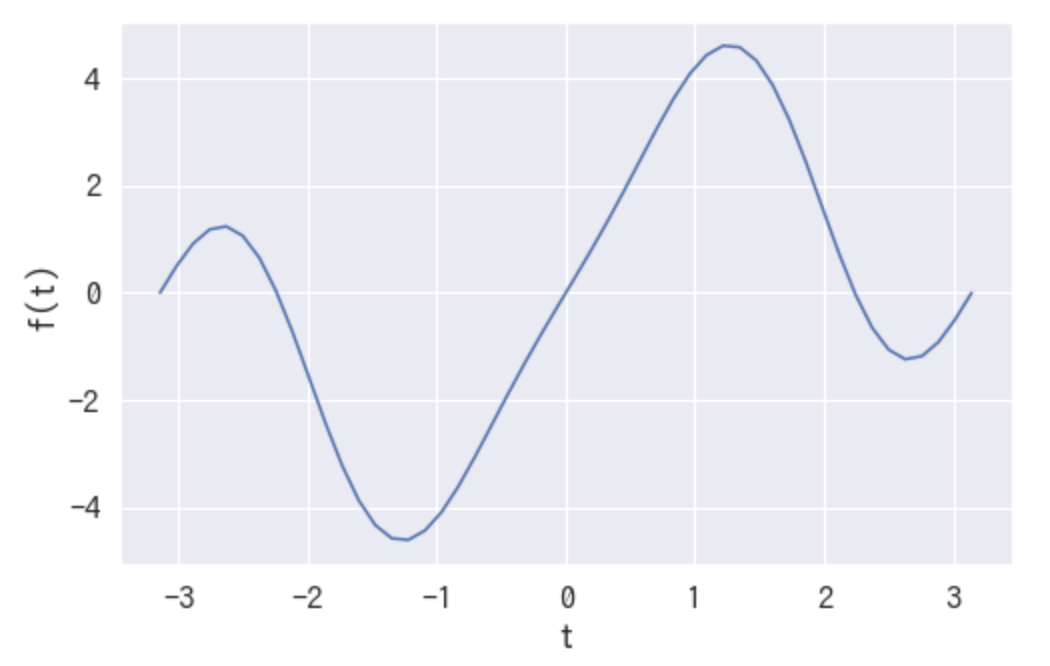
(これはもちろん私が作ったので事前に知ってるだけですが)調べたら下記の式で表せることがわかりました。
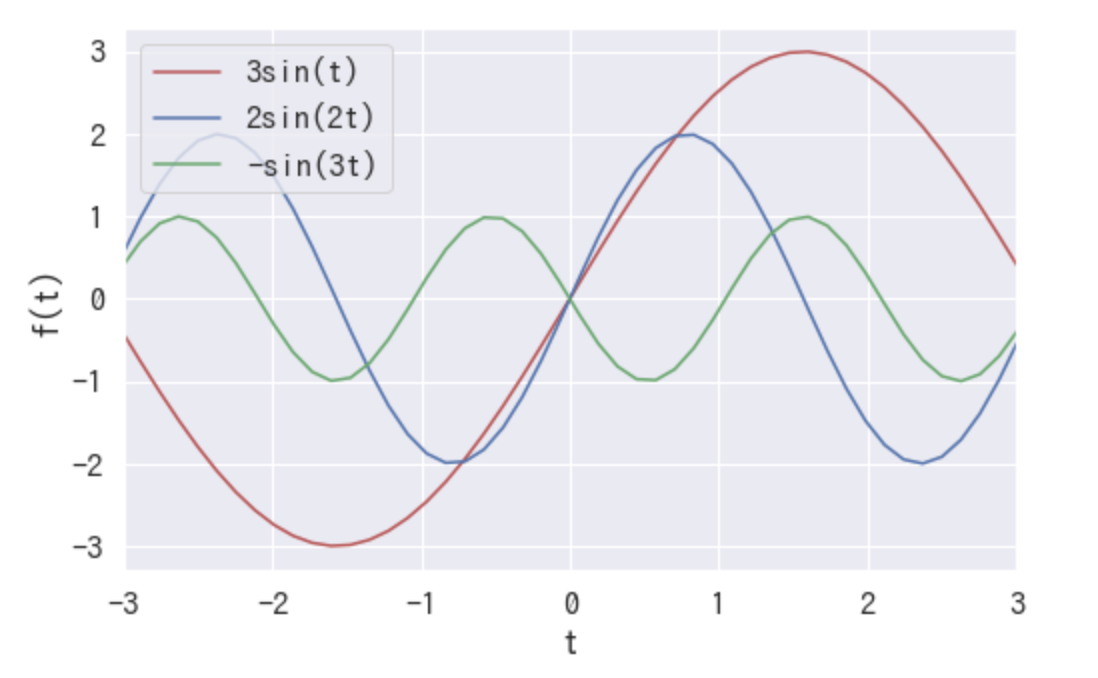
このようにマクローリン展開などと違って、sinやcosなどの三角関数の和で関数近似しようというのがフーリエ級数展開の特徴です。 季節性の売上など、周期性をもった波形のデータであれば
ここまでの話をまとめるため、少し強引に一般化した式に直すと
三角関数の周波数について
Prophetの季節関数を理解するためにあと一点だけ、周波数の部分について深掘っていきます。
周波数はsin波cos波の振幅数を表しています。
という単位で一周するので、例えば30日のうち1週間ごとに一周するsin波を表現したい場合は
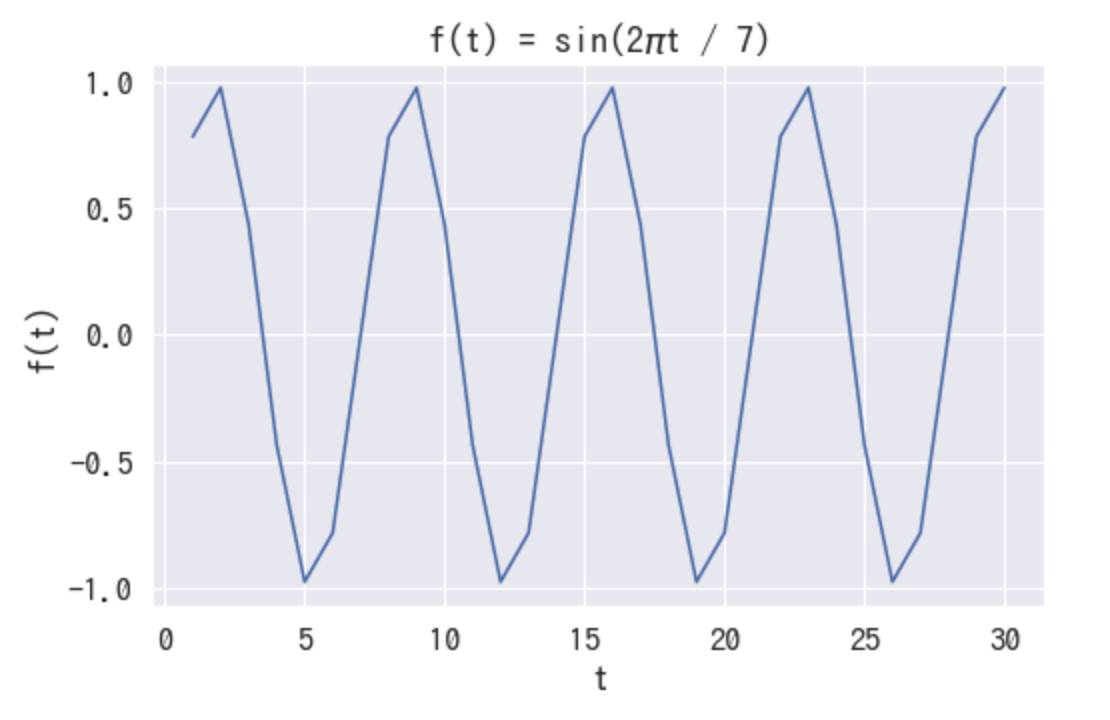
Prophetの季節関数では、このような週、月、年単位の周期を持つことを柔軟に表現できるよう変数 を用いて
パラメタ推定しやすい形に変形する
このとき最適化すべきは ] の部分、合計2N個のパラメタなので扱いやすいベクトルで抜き出して表現します。
残りの三角関数の部分もベクトル化して抜き出します。仮にの粒度までで関数近似し、年単位の季節変化に見るために
とした場合には、
※ 閏年を含めると1年の平均日数は365.25
これらを用いて結局 は下記のように変形できます。
ちなみにパラメタは多いほど周期変動にうまく当てはまるようになりますが、同時にオーバーフィッティングしてしまう問題も抱えています。論文では、年単位の周期なら
、週単位なら
くらいで程よくフィッティングすると書いてあります(個人的にN = 10 はやや多いのでは、という気もしますが)。
3.  : 休日効果
: 休日効果
最後に突発的なイベント効果をモデルに組み込む について見ていきます。
これも英語の直訳で「休日効果」と書きましたが、意味的には休日含むイベント全てを
で扱えます。
休日やイベントの多くは事前に予見できるわりに周期といったものはなく、季節変化 では取り入れにくい要素です。そのため自動検知云々は諦め、Prophetでは分析者自身がイベントカレンダーのリストを作ってモデルに組み込めるように設計しています。
この設計をProphetではどのような数式で表しているのかを見ていきます。
あるイベントをとし、それに該当する日付を全て含んだベクトル
を作ります。
たとえば
なら
各イベント
まとめ
冒頭のProphetのモデル式を再掲すると下記のような、主に3つのコンポーネントからできていました。
各要素は最終的に下記のように展開できました。
...本当はこれら未知のパラメタの最適化について書かないとキリが悪いのですが、もう体力が記事のボリュームが限界なので簡単に述べます。
諸々のパラメタを定義していく中で、記事中では下記の3つについてわざわざ確率分布を仮定していました。
最後に
私自身が数学があまり得意でないのでかなり噛み砕いて書いてみました。どなたかの理解のとっかかりになれば幸いです。
明日のアドベントカレンダーは Owners Growthチームの大木さんと、PAY株式会社のセキュリティエンジニア、クリスさんです!
お楽しみに!